
孤立森林(Isolation Forest)是周志华团队于2008年提出的一种具有线性复杂度的异常检测算法,被工业界广泛应用于诸如异常流量检测,金融欺诈行为检测等场景。
算法原理
异常检测领域,通常是正常的样本占大多数,离群点占绝少数,因此大多数异常检测算法的基本思想都是对正常点构建模型,然后根据规则识别出不属于正常点模型的离群点,比较典型的算法有One Class SVM(OCSVM), Local Outlier Factor(LOF)。和多数异常检测算法不同,孤立森林采用了一种较为高效的异常发现算法,其思路很朴素,但也足够直观有效。
考虑以下场景,一个二维平面上零零散散分布着一些点,随机使用分割线对其进行分割,直至所有但点都不可再划分(即被孤立了)。直观上来讲,可以发现那些密度很高的簇需要被切割很多次才会停止切割,但是密度很低的点很快就会停止切割到某个子空间了。

孤立森林分训练和异常评估两部分:
- 训练: 根据样本抽样构建多棵iTree,形成孤立森林
- 异常评估: 根据训练过程构建的孤立森林,计算待评估值的异常得分
训练
- 给定训练数据集\(X\),确定需要构建的孤立树(iTree)个数t,按\(\phi\)采样大小随机取样作为子样本集\(X^{'}\)
- 在子样本集\(X^{'}\)上构建一棵孤立树(iTree),过程如下图所示:

在\(X\)中随机选择一个属性(维度),在当前样本数据范围内,随机产生一个分割点\(p\)(介于当前维度最大和最小值之间)
此切割点即是一个超平面,将当前节点数据空间切分成2个子空间:将当前所选维度下小于p点的放在当前节点左分支,把大于p点的放在当前节点的右分支
在节点的左分支和右分支递归执行步骤a,b,不断构造新的叶子节点,直到叶子节点上只有一个数据或者树已经生长到了限制的高度
单棵iTree构建完成
- 按2的过程,依次构建t棵iTree,得到孤立森林

异常评估
构建了孤立森林(IForest)后,可以评估某个点\(x\)的异常得分,用到如下公式:
\[s(x,n)=2^{-\frac{E(h(x))}{c(n}} \]
其中,\(h(x)\) 表示\(x\)在某棵孤立树中的路径长度,\(E(h(x))\) 表示在所有孤立树中的期望路径长度。\(c(n)\) 为样本数为n时的二叉排序树(BST)的平均搜索路径长度,用来对样本\(x\)的期望路径长度做归一化处理。\(c(n)\)公式如下:
\[c(n)=2H(n-1)-(2(n-1)/n)\]
其中,\(H(i)\)是一个调和数,约等于 \(ln(i) + \gamma\),\(\gamma\)为欧拉常数,约等于0.5772156649
论文对于异常得分分布有如下结论:
如果异常得分接近1,那么一定是异常点
如果异常得分远小于0.5, 那么一定不是异常点
如果样本点的异常得分均在0.5左右,那么样本中可能不存在异常点
异常得分\(s\)和\(E(h(x))\)关系图如下所示

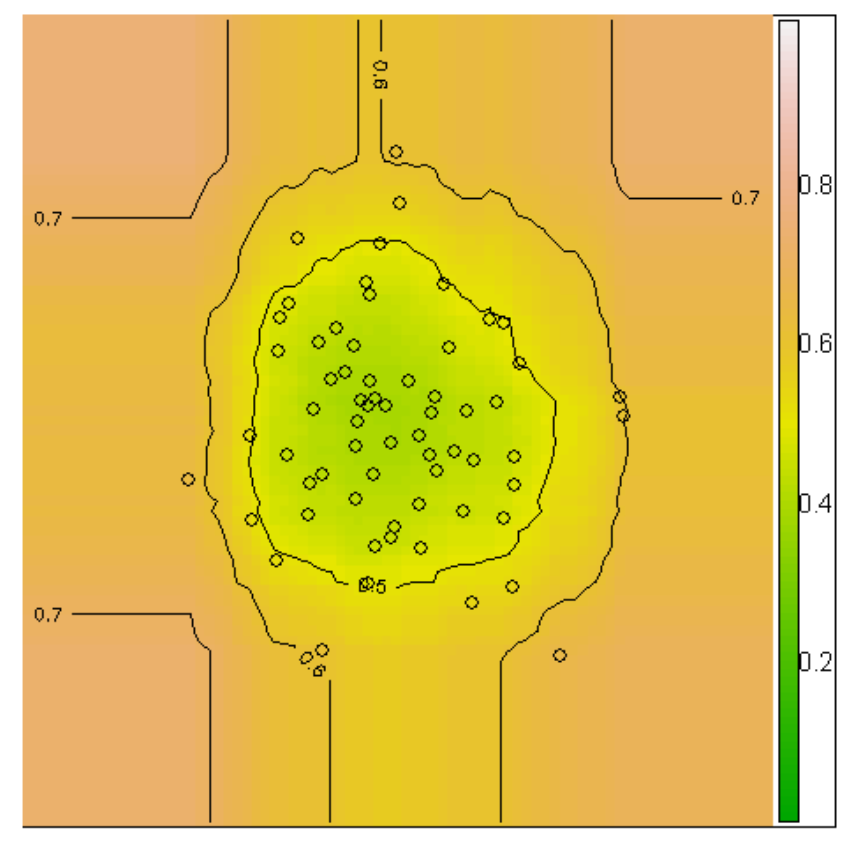
异常得分的等高线图如下所示,通常潜在的异常点\(s>=0.6\)
参考资料
1.Liu F T, Ting K M, Zhou Z H. Isolation forest[C]//2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008: 413-422.